Сегодня рассмотрим, чем отличаются подходы к представлению данных в глубоком машинном обучении и реляционной логике, как это связано с декларативной парадигмой логического программирования и при чем здесь графы. А в качестве примера реализации этих идей рассмотрим комбинацию принципов Deep Learning с реляционной логикой и GNN-нейросетями в Python-библиотеке PyNeuraLogic.
Машинное обучение и реляционная парадигма
Хотя тема глубокого машинного обучения сегодня очень популярна, такие системы пока еще являются скорее экзотикой, чем устоявшейся практикой, активно применяемой в производстве. Помимо развивающегося математического аппарата и высоких требований к аппаратному обеспечению, одним из барьеров, затрудняющих повсеместное внедрение Deep Learning, является невозможность представить огромный объем обучающих данных в популярной парадигме реляционных СУБД. Сегодня в большинстве ML-фреймворков и библиотек обучающие данные для ML-моделей представляются в виде числовых тензоров, то есть n-мерных массивов чисел. Это сводится к традиционному обучающему представлению векторов признаков, образуя одномерный случай этих тензоров.
Исторически, независимо от домена, все классические модели машинного обучения были разработаны для ввода векторов признаков. Сперва требовалось определить характерные признаки бизнес-проблемы, собрать ряд из них в вектор и выполнить повторные измерения этих векторов признаков, чтобы создать достаточно большой набор обучающих данных. В отличие от классического Machine Learning, глубокое обучение устраняет необходимость ручного проектирования входных фичей, заменив их большими объемами необработанных данных. Характерные фичи возникают в процессе самого обучения и называются встраивания (embedding), представляя собой числовые векторные представления объектов, встроенные в общее n-мерное пространство. При этом представление обучения на самом деле остается в виде числовых векторов (тензоров).
Графовые алгоритмы. Бизнес-приложения
Код курса
GRAF
Ближайшая дата курса
20 мая, 2024
Продолжительность
24 ак.часов
Стоимость обучения
54 000 руб.
Однако, это представление далеко не универсально, поскольку реальные данные реального мира хранятся не в числовых векторах или тензорах, а во взаимосвязанных структурах интернет-страниц, социальных сетей, графов знаний, сведений о биологических, химических и инженерных объектах и пр. По сути, это реляционные данные, которые естественным образом хранятся в структурированной форме графов. Поэтому возникает очевидный вопрос: можно ли превратить эти структуры данных в векторы признаков (числовые тензоры) и напрямую использовать их в Machine Learning и глубоком обучении? Но, при всей привлекательности этого подхода, у него есть следующие недостатки:
- нет простого способа превратить несвязанную реляционную структуру данных в обычный числовой тензор фиксированного размера без потери информации. Хотя тензор тоже является примером реляционной структуры данных, представляя собой сетку. Но это становится проблемой, если примерный тензор больше ожидаемого входа модели.
- даже если ограничиться ограниченными представлениями, существует принципиальная проблема неоднозначности такого преобразования, вытекающая из присущей реляционным структурам симметрии.
Впрочем, если бы существовало однозначное инъективное отображение между графами и тензорами, оно тривиально решило бы (жесткую) проблему изоморфизма графов. А, чтобы избежать потери информации и двусмысленности, которые ведут к серьезной неэффективности машинного обучения, при превращении графовых структур в векторы, снова возникает вопрос созданию признаков.
Для этого есть много способов, таких как агрегирование (подсчет) объектов, отношений, различных шаблонов (подграфов) и их статистики, называемое извлечением реляционных признаков. Реализация этих способов может быть автоматизирована, но их идея несовместима с основной идеей глубокого обучения. Решить проблему применения принципов Deep Learning к реляционным структурам поможет передача больших данных в трансформерную архитектуру нейросетей.
Чтобы понять, как это работает, сперва рассмотрим векторное представление обучающих данных с позиции реляционной парадигмы. Такие данные также можно представить в виде таблицы, где каждый столбец соответствует признаку (или целевой метке), а каждая строка соответствует одному независимому обучающему примеру — вектору признаков. Следовательно, можно хранить векторы признаков в любой базе данных с помощью всего одной таблицы. А если векторы признаков зависят друг от друга, т.е. один элемент в одном векторе признаков может фактически представлять тот же объект, что и другой элемент в другом векторе признаков, такие векторы можно использовать для представления перекрывающихся последовательностей данных временных рядов, слов в предложении, предметов в корзине или фигур на шахматной доске. Во всех этих случаях элементы векторов нельзя рассматривать как простые независимые значения, а как ссылки на базовые объекты, которые затем несут фактические фичи.
Поэтому получается 2 таблицы, где первая содержит, возможно, повторяющиеся ссылки на объекты во вторую таблицу, которая содержит (уникальные) значения характеристик объектов. Напомним, в формальной терминологии баз данных таблица также называется отношением, так как она связывает объекты из столбцов вместе. Рассматривая такие векторы как последовательности объектов, можно обобщить их длины, чтобы использовать в моделях последовательностей, таких как рекуррентные нейронные сети. А разветвление таких последовательностей приведет к представлению данных в виде дерева, например, дерева синтаксического анализа предложений, и рекурсивных нейросетей. Также можно обобщить данные, структурированные на основе графа, что сводится к представлению современных нейросетевых архитектур, включая трансформеры. Хотя технически они принимают последовательности на входе, под капотом это превращается в полносвязные графы, предполагая все парные отношения элементов в модуле (само)внимания.
Примечательно, что все эти модели попадают под реляционный формализм, являясь примерами обработки бинарных отношений. Это означает, что для хранения графа (последовательности, дерева) в базе данных достаточно создать единую таблицу с двумя столбцами, соответствующими двум узлам, соединенным ребром. Тогда каждый граф представляет собой просто набор таких ребер, каждое из которых хранится в отдельной строке. Для графов с различными метками связанные атрибуты могут быть снова эффективно сохранены в таблице с отдельными ссылками, как и раньше. Пример представления такой структуры данных в реляционном и графовом виде я описывала здесь.
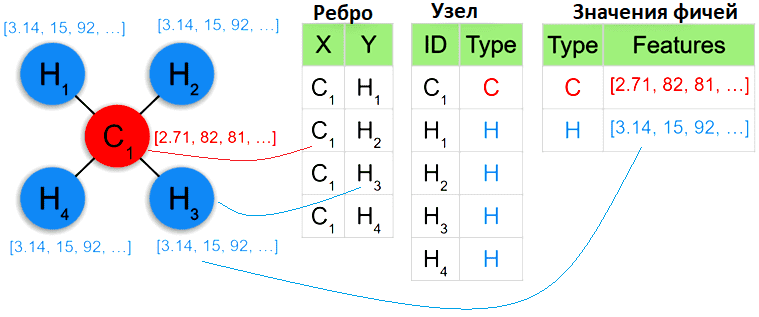
Однако, одна строка больше не соответствует одному экземпляру обучающих данных, поскольку могут быть примеры различных размеров и структур, охватывающих несколько таблиц через ссылки на объекты. Впрочем, реляционные базы данных не ограничиваются бинарными отношениями, поскольку таблица может связать более двух объектов, т. е. каждая таблица является гиперграфом. Таким образом, все часто используемые представления машинного обучения могут быть зафиксированы в реляционной логике, что делает ее возможным для практического использования. Как это реализовать, рассмотрим далее.
Логическое программирование и реляционные модели в глубоком обучении
Интересно, что идея применить реляционную логику в машинном обучении не нова. Реляционные методы обучения, такие как индуктивное логическое программирование (ILP), представляют собой способ изучения эффективных и интерпретируемых моделей. Этот подход демонстрирует общность формализма реляционной логики, который используется не только для захвата данных и обучающих представлений, но и для самих моделей, обеспечивая включение фоновых знаний и симметрии предметной области.
Полученные модели естественным образом позволяют учиться на основе баз данных, где разные выборки состоят из разных типов и количества объектов, причем каждый объект характеризуется различным набором атрибутов, охватывающим несколько взаимосвязанных таблиц. Хотя это стандарт для ILP, такому подходу не хватает надежности, точности и масштабируемости, чего требует глубокое обучение.
Комбинируя парадигму реляционной логики с принципами Deep Learning, можно получить новый декларативный язык шаблонов, который позволяет кодировать модели глубокого обучения, сохраняя выразительность реляционных логических представлений и выводов. Примером реализации этого подхода являются графовые нейросети (GNN), которые активно используются сегодня в медицине и биохимии.
В основе любой GNN-модели лежит так называемое правило распространения для передачи сообщений (представлений) между соседними узлами. Представление узла X вычисляется путем агрегирования предыдущих представлений соседних узлов Y, тех, у которых есть ребро между X и Y. Это похоже на декларативную парадигму логического программирования, где объявляются логические переменные и отношения между ними, которые потом могут быть объединены в так называемые правила, управляющие вычислениями. Такой набор правил формирует логическую программу, и ее выполнение эквивалентно выполнению логического вывода с помощью правил.
Инструментально эти идеи воплощены в открытой Python-библиотеке PyNeuraLogic, которая позволяет писать программы дифференциальной логики на самом популярном в мире Data Science языке программирования. PyNeuralogic через свой бэкенд NeuraLogic делает процесс вывода дифференцируемым, что эквивалентно прямому распространению в глубоком обучении. Это позволяет изучать числовые параметры, которые можно связать с правилами, аналогично весам в нейросетях.
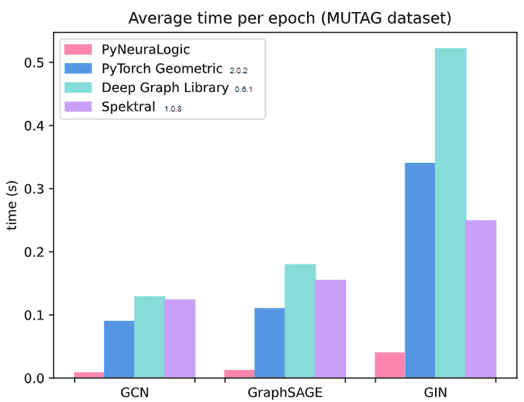
Впрочем, PyNeuralogic не ограничивается GNN-моделями, поскольку выразительность реляционной логики выходит за рамки графов. Можно работать с несколькими отношениями и типами объектов, гиперграфами, вложенными графами, реляционными базами данных и пр. В PyNeuraLogic все эти идеи принимают одну и ту же форму простых небольших логических программ, которые просты благодаря своей декларативной природе. Нет необходимости проектировать множество классов для каждой небольшой модификации правила GNN — все кодируется непосредственно на уровне логических принципов. А внутренней движок этой библиотеки создает базовые графы дифференцируемых вычислений (выводов) полностью автоматизированным и динамическим способом, позволяя ML-инженеру не волноваться о преобразовании данных в статические (тензорные) операции. Эксперименты показали, что PyNeuraLogic работает быстрее многих GNN-платформ на базе PyTorch и других Deep Learning фреймворков.
Как применять эти и другие современные инструменты MLOps в проектах аналитики больших данных, вы узнаете на специализированных курсах в нашем лицензированном учебном центре обучения и повышения квалификации для разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data в Москве:
Источники