В прошлой статье мы разобрали методы построения рекомендательных систем:
- коллаборативная фильтрация;
- фильтрация на контенте;
- фильтрация на знаниях;
- гибридный подход.
Мы намеренно не упомянули об одном важном подходе построения рекомендаций: об использовании матричных разложений. Описание данного метода заслуживает отдельной статьи!
Будем эксплуатировать традиционный для рекомендательных систем кейс рекомендации фильмов пользователям. Напомним, что в нашем распоряжении есть пользователи и их оценки фильмам. Рекомендательная система по данной информации должна предоставлять пользователям рекомендации фильмов, которые с высокой вероятностью должны им нравиться.
Информацию об оценках фильмов удобно представлять в виде матрицы, где строки соответствуют пользователям, а столбцы фильмам. На пересечении строки и столбца будет оценка пользователем соответствующего фильма.
Рисунок 1.
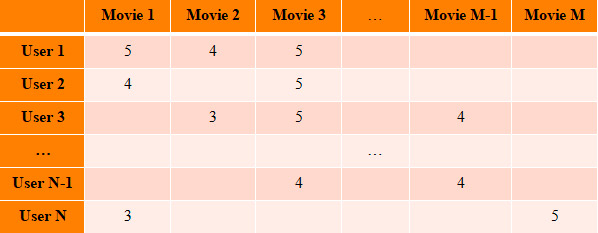
Матрица выше имеет прямоугольную форму, так как обычно значение M не совпадает с N (количество пользователей с малой вероятностью совпадает с количеством фильмов). Ее называют user-item матрицей или UI матрицей. Именно с ней нам предстоит работать. Отвлечемся на то, чтобы вспомнить чуть-чуть математики.
SVD разложение
Сингулярное разложение матриц (SVD-разложение) – это представление прямоугольной матрицы в виде произведения нескольких матриц особого вида. Цель этого разложения – это упростить некоторые вычисления, которые будут осуществляться над матрицей. Цель в контексте рекомендательных систем и нашего примера с фильмами состоит в том, чтобы по полученному представлению мы могли получить прогноз оценки пользователя.
Если говорить формально, то любая прямоугольная матрица размеров N на M представляется в виде:
![]()
где U и V – унитарные матрица порядка N и M соответственно (при этом матрица V* — это сопряженно-транспонированная матрица к V), Σ – матрица размеров NxM, на главной диагонали которой лежат неотрицательные числа (называются сингулярными числами матрицы, откуда и пошло название разложения). Выдохнем и не будем вдаваться в суть определений. Что значит данное разложение для нас?
SVD разложение для получения рекомендаций
Благодаря SVD-разложению мы можем представить UI матрицу в виде:
![]()
где матрица в некотором смысле матрица U будет представлять пользователей, а матрица V фильмы. Другими словами, строки матриц U будут являться представлениями пользователей, а столбцы матрицы V фильмов.
Рисунок 2.
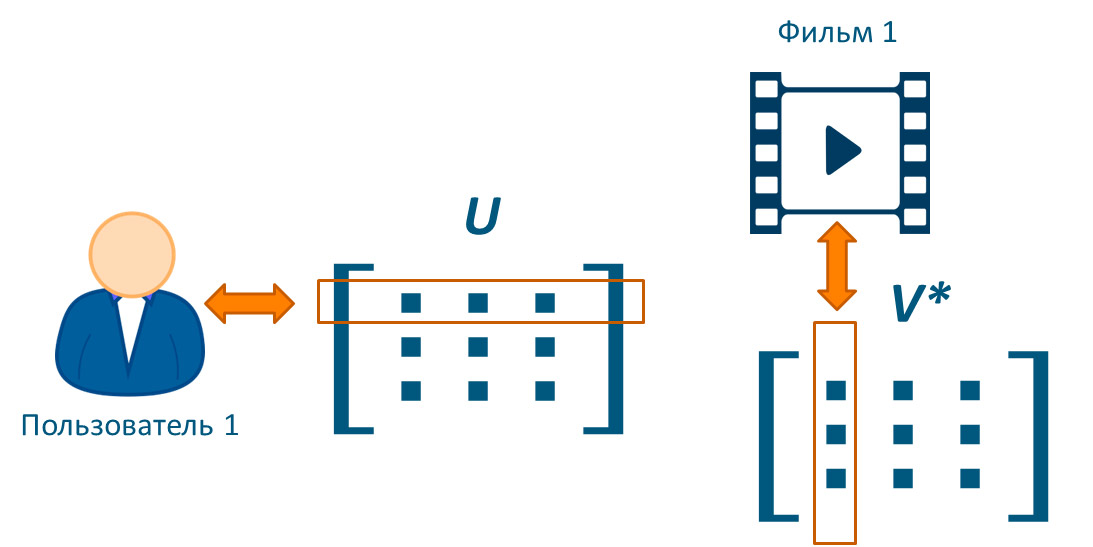
Чтобы получить оценку фильма j пользователя i необходимо iю строку матрицы U умножить по правилу умножения матриц на jй столбец матрицы V*, взвесив полученное линейной соотношение на коэффициенты диагонали матрицы Σ.
В итоге следующая ситуация. У нас есть частично заполненная UI матрица историческими оценками пользователей. Наша задача заполнить все остальные пустые места (со знаками вопроса на рисунке 3) UI матрицы.
Рисунок 3.
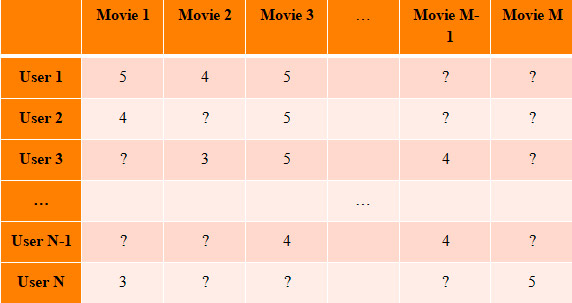
Для этого по частично заполненной UI матрицы мы приближенно вычислим SVD разложение UI матрицы и далее найдем оценки фильмов перемножив матрицы полученного разложения. Ответ на вопрос как искать приближенное SVD разложение матрицы по информации о части ее элементов появился в результате известного конкурса Netflix, о котором мы писали в первой статье.
Поиск приближенного SVD разложения
Для поиска приближенного SVD разложений Саймон Функ предложил минимизировать следующий функционал:
![]()
![]()
где ui, vj строки и столбцы матриц U и V* соответственно, mati,j– известные элементы UI матрицы. Минимизация может производиться различными математическими методами, например, с помощью градиентного спуска.
Метод Саймона Функа имел успех в конкурсе и в дальнейшем был реализован в компании Netflix. Вместе с тем отметим, что при большом количестве пользователей и фильмов мы столкнемся с задачей минимизации большого функционала. Эта задача сложно решаема на больших объемах. На практике обычно либо ограничиваются размерами представлений пользователей и фильмов – параметрически задают длину строк матрицы U и соответственно длину столбцов матриц V*, либо выполняют кластеризацию пользователей или фильмов.
Некоторые практические детали реализации изложенного подхода в библиотеках на python можно узнать из видео.